Hai hai semua ^_^ Aye Admin K. Di postingan ini, aye bakal ngebahas lagi soal matematika. Soal yang aye bahas di post ini adalah salah satu soal AHSME tahun 1983. Soal ini adalah soal mencari bilangan terkecil yang bisa diselesaikan dengan berbagai cara yang salah satunya adalah menggunakan turunan. Langsung saja, kita lihat soalnya.
Problem 21
Find the smallest positive number from the numbers below.
(A) (B)
(C)
(D)
(E)
Terjemahan
Carilah bilangan positif terkecil dari bilangan-bilangan berikut.
(A) (B)
(C)
(D)
(E)
Solusi
Perhatikan soal baik-baik. Soal menyuruh untuk mencari bilangan positif. Dengan demikian, kita harus cek apakah ada bilangan negatif atau 0 di opsi (tidak ada 0 di opsi). Perhatikan opsi (A) adalah negatif dari opsi (B). Berarti, salah satu dari (A) atau (B) adalah bilangan negatif. Mari kita tinjau satu persatu.
Untuk opsi (A), karena yang merah lebih besar daripada yang biru. Itu artinya opsi (A) adalah salah satu kandidat jawaban. Untuk opsi berikutnya:
(B)
(C)
(D)
(E)
Jelas bahwa, kandidat jawaban di antara (A) atau (D). Selanjutnya, tinggal dibandingkan, mana yang lebih kecil, apakah atau
. Ada beberapa cara yang bisa digunakan. Salah satunya adalah dengen memanfaatkan turunan fungsi. Bagaimana caranya? Perhatikan kembali kedua kandidat jawaban yang bisa ditulis kembali sebagai berikut.
(A)
(D)
Tampak bahwa kedua jawaban mengikuti pola fungsi . Kita bisa meninjau naik turunnya fungsi tersebut dengan menggunakan turunan. Turunan dari fungsi tersebut adalah
.
Dengan menggunakan power rule (aturan pangkat) dan chain rule (aturan rantai), diperoleh
Samakan penyebut dengan mengalikan dan
masing-masing pada pembilang dan penyebut berturut-turut pada suku pertama dan kedua.
Nah, perhatikan bahwa untuk , selalu berlaku
sehingga
. Selain itu, berlaku pula
dan
(ingat nilai akar non-negatif). Dengan demikian, saat
, pembilang dari
bernilai negatif dan penyebutnya bernilai positif. Walhasil,
bernilai negatif. Ini menunjukkan bahwa
adalah fungsi monoton turun (tegas) saat
.
Akhirnya, karena , mengingat
fungsi turun, maka
atau
. Dengan kata lain,
(yakni, jawaban (D)) lebih kecil dari
(jawaban (A)). Jadi, dapat disimpulkan bahwa jawaban dari soal adalah (D) sebab
adalah bilangan positif yang terkecil.
Eitss, gak harus pake turunan lho. Masih ada cara lain.
Solusi Alternatif
Perhatikan bahwa
Kalikan, bagian pembilang (bisa menggunakan rumus beda kuadrat)
.
Dengan cara yang serupa, diperoleh juga
Perhatikan bahwa penyebut lebih besar dari penyebut
. Dengan demikian
atau dengan kata lain, kesimpulannya sama seperti solusi menggunakan turunan sebelumnya yakni
. Cara kedua selesai, terbukti lagi bahwa jawaban (D) benar. Satu masalah, punya banyak solusi. Kalian bisa memilih solusi mana yang kalian suka tergantung selera.
Jadi, gimana? Fun dan emejing, bukan? Solusi mana yang kalian suka? Semoga bermanfaat dan semoga kalian enjoy. Kalo ada komentar, tanggapan, koreksi, pertanyaan, atau mungkin ada cara lain, silakan sampaikan di kolom komentar. Sampai jumpa di postingan selanjutnya. Bye~

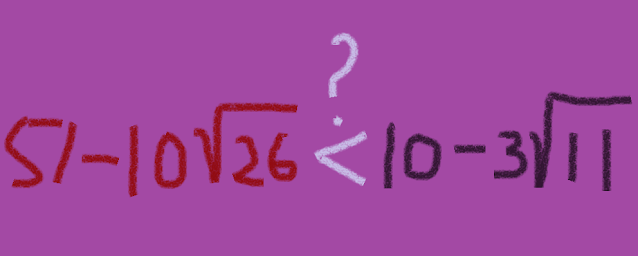








No comments:
Post a Comment