Wednesday, August 14, 2024
Friday, June 21, 2024
Hai hai semua ^_^ Aye Admin K kembali lagi setelah sekian lama ga nulis di blog ini. Kali ini aye kembali lagi ngebahas soal matematika. Soal yang bakal aye bahas kali ini ini adalah soal berikut ini.
Tunjukkan bahwa jika \( \left | z \right | = 1 \) atau \( \left | w \right | = 1 \), dan \( \overline{z} w\), maka berlaku
\( \left | \frac{z-w}{1 - \overline{z} w} \right | = 1 \).
Saturday, February 10, 2024
Monday, January 15, 2024
Seperti yang kita tahu bahwa kecepatan loading website menjadi salah satu pertimbangan bagi mesin pencari untuk menentukan peringkat sebuah situs web atau blog. Di internet sudah ada banyak yang memposting tutorial cara mempercepat ataupun meringankan loading website dan silahkan kamu dapat menerapkan kesemua cara tersebut. Saya cenderung lebih suka menerapkan beberapa hal yang memang bisa memberikan dampak kecepatan loading website secara signifikan. Saya pribadi pun sudah menerapkan sekian banyak tips dan trik yang saya temukan di internet. Namun saya rasa tidak kesemua cara tersebut memberikan dampak yang signifikan. Intinya semakin kecil jumlah data yang di load oleh website maka loadingnya akan semakin cepat.. Jadi, wajib bagi kamu untuk membuat halaman web beserta konten yang ringan seperti gambar yang di kompres.
Saturday, October 7, 2023
Panglima TNI, Laksamana TNI Yudo Margono, telah melakukan mutasi, rotasi, dan promosi terhadap 156 perwira tinggi TNI. Mutasi ini mencakup sejumlah jabatan penting seperti Komandan Korps Marinir (Dankormar) TNI AL, Inspektur Jenderal (Irjen) TNI, dan Oditur Jenderal (Orjen) TNI. Kebijakan mutasi tersebut diumumkan melalui Surat Keputusan Panglima TNI Nomor Kep/1127/X/2023 yang diterbitkan pada 2 Oktober 2023.
Monday, August 7, 2023
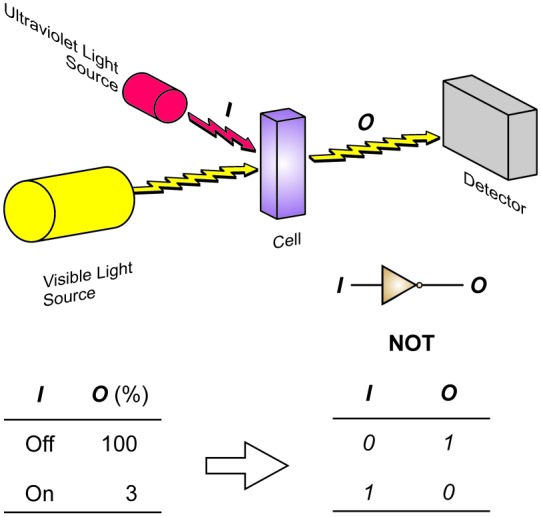
Transisi bertahap dari jaringan listrik ke jaringan optik menyertai kemajuan pesat teknologi telekomunikasi. Dorongan untuk meningkatkan kapasitas dan kecepatan transmisi mengendalikan tren ini. Faktanya, volume besar data yang dikodekan pada sinyal optik dapat diangkut dengan cepat melintasi jarak yang jauh. Propagasi sinyal optik sepanjang rute tertentu di seluruh jaringan komunikasi dijamin oleh kombinasi serat optik dan sakelar optoelektronik. Namun, tampaknya interaksi antara rangsangan listrik routing dan sinyal optik yang bergerak tidak akan mampu mendukung kapasitas terabit-per-detik yang akan dibutuhkan dalam waktu dekat. Masukan listrik tidak dapat menangani paralelisme besar yang potensial dengan sinyal optik. Prinsip operasi untuk mengendalikan sinyal optik dengan sinyal optik harus dikembangkan. Sakelar molekuler dan supramolekuler adalah kandidat yang menjanjikan untuk mewujudkan bahan inovatif untuk teknologi informasi. Digit biner dapat dikodekan dalam masukan dan keluaran kimia, listrik, atau optik mereka untuk menjalankan fungsi logika tertentu. Kami telah mengembangkan strategi sederhana untuk mengendalikan sinyal optik dengan sinyal optik dengan menggunakan sakelar molekuler fotoaktif. Kami telah menunjukkan bahwa operasi NAND, NOR, dan NOT dapat diimplementasikan secara eksklusif dengan masukan optik dan keluaran optik yang menghubungkan dari satu hingga tiga elemen sakelar. Pendekatan kami yang sangat sederhana untuk pengalihan pemrosesan optik total mungkin akan mengarah pada pengembangan generasi baru perangkat untuk teknologi pemrosesan dan komunikasi digital.
Saturday, August 5, 2023
Hai hai semua ^_^ Aye Admin K. Ini adalah postingan lanjutan dari postingan sebelumnya tentang pengertian definit positif dan negatif dari fungsi kuadrat serta syaratnya kapan bisa menjadi definit positif atau negatif. Nah, karena ada rikues dari komentar, di postingan kali ini, aye bakal memberikan dua contoh soal tentang topik ini yakni mengenai definit positif dan negatif dari fungsi kuadrat. Baiklah, daripada lama-lama, mending kita mulai dari soal yang pertama.
Saturday, July 1, 2023
 |
| sumber: formula1.com |
Max Verstappen berpendapat bahwa para pembalap Formula 1 terlihat seperti "amatir" dan "bodoh" akibat serangkaian pelanggaran batas lintasan selama sesi kualifikasi Grand Prix Austria 2023.
Pembalap yang menjadi juara dua kali berturut-turut ini meraih pole position keempat secara beruntun di Red Bull Ring dengan mencatat waktu 1m04.391s. Ia unggul 0.048 detik dari pembalap Ferrari, Charles Leclerc.
Friday, February 17, 2023
Thursday, February 9, 2023
If you have an ATV, you know how expensive the hobby can be. ATV’s can be very expensive and the parts and costs of maintenance can also be high. If you have to do emergency repairs of even replace a badly damaged ATV you may find yourself strapped for cash. The initial ATV purchase is also a major expense, especially if you buy new. It is possible to save money, keep to a budget, and enjoy ATV riding. You should still be prepared to invest money in your hobby but if you do some research, you can find good prices on ATV’s and ATV parts.
Thursday, February 2, 2023
There will be days when you bring the new baby home that you think you’ll never get to sleep again. In the meantime, try to get some rest and sleep whenever you can. The baby won’t be sleeping through the night for several weeks, perhaps months. While the baby is adjusting to the schedule of night and day, you won’t be able to sleep through the night until the baby does.
Anybody could own a web site. Anybody could up sell their own products and services to their target audience. Anyone could try to promote their web site with a low cost. But there are not many web sites that have a truly successful web site with traffic all day through. What these individuals or companies lack is the most essential factor of success – a low cost web site promotion that really works.
Sunday, September 25, 2022
Hai hai semua ^_^ Aye Admin K. Kembali lagi di blog kesayangan kita, KnK Land. Kali ini, aye hanya akan memberikan postingan singkat aja yakni daftar nama-nama mata pelajaran di sekolah dalam bahasa Arab. Postingan ini sangat cocok buat kalian yang lagi sekolah dan ada mata pelajaran bahasa Arabnya atau sekolah di madrasah. Dengan membaca postingan ini, kalian bisa pamer ke teman-teman kalian kalau kalian tahu banyak kata. Kalian juga bisa pamer tulisan jadwal kalian di buku yang pakai bahasa Arab. Nah, langsung aja nih, cekidoot.
A gradual transition from electrical to optical networks is accompanying the rapid progress of telecommunication technology. The urge for enhanced transmission capacity and speed is dictating this trend. In fact, large volumes of data encoded on optical signals can be transported rapidly over long distances. Their propagation along specific routes across a communication network is ensured by a combination of optical fibers and optoelectronic switches. It is becoming apparent, however, that the interplay between the routing electrical stimulations and the traveling optical signals will not be able to support the terabit-per-second capacities that will be needed in the near future. Electrical inputs cannot handle the immense parallelism potentially possible with optical signals. Operating principles to control optical signals with optical signals must be developed. Molecular and supramolecular switches are promising candidates for the realization of innovative materials for information technology. Binary digits can be encoded in their chemical, electrical, or optical inputs and outputs to execute specific logic functions. We have developed a simple strategy to gate optical signals with optical signals by using a photoactive molecular switch. We have demonstrated that NAND, NOR, and NOT operations can be implemented exclusively with optical inputs and optical outputs coupling from one to three switching elements. Our remarkably simple approach to all-optical switching might lead to the development of a new generation of devices for digital processing and communication technology.
Friday, September 16, 2022
Hai hai semua ^_^ Aye Admin K. Kembali lagi di blog kesayangan kita semua, KnK Land. Kali ini aye akan membahas sedikit mengenai salah satu indomaret versi Swiss. Kenapa aye membahas ini? Karena tentu saja aye sangatlah random serta memperkaya kata kunci di blog ini. Mari langsung aja kita cekidoot.